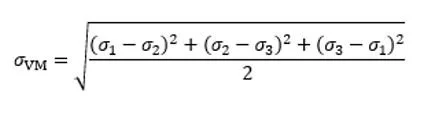ASME B&PV Code Protection Against Local Failure: What Is It and Why Is It Important?
The Design-by-Analysis requirements of Part 5 of Section VIII, Division 2 of the ASME Boiler & Pressure Vessel Code lists four failure modes that must be considered when evaluating pressure vessels. They are: plastic collapse, local failure, buckling, and cyclic loading (fatigue).
Imagining how a pressure vessel can fail due to excessive plastic deformation (plastic collapse), buckling, or fatigue is not too difficult. But what does the Code mean by local failure? Evaluations for protection against plastic collapse almost always show the critical areas are local to some structural discontinuity, such as at the junction of a nozzle and shell. Buckling can be localized, and fatigue is a local stress phenomenon. So, what exactly is the failure mechanism being considered in evaluating a component for local failure and why is it important?
Brittle Failure of Otherwise Ductile Materials
The short answer is evaluating for protection against local failure is done to ensure the component does not fail due to hydrostatic stress. Hydrostatic stress in this case does not mean stresses caused by hydrostatic pressure, such as when a pressure vessel is filled with a liquid. Rather it refers to the stress state where there are equal normal stresses along all three orthogonal axes. This stress state occurs when an object is immersed in a fluid, which is why this stress state is often referred to as hydrostatic stress.
The reason for evaluating hydrostatic stresses is when ductile materials are subjected to hydrostatic tensile stresses, they can rupture with no prior plastic deformation. In other words, they behave as brittle materials. Furthermore, this type of failure will never be predicted when evaluating a component for protection against plastic collapse using the ASME Code.
When Local Failure Occurs and Why It Won’t be Predicted using Equivalent Stress
The total stress in a material can be separated into two components. One component relates to the change in volume of the material (known as the hydrostatic or volumetric stress), the other to the change in shape of the material (deviatoric stress).
The deviatoric stress is important in that it is used in predicting the onset of yielding and ductile failure. Equivalent (von Mises) stress relates the deviatoric stress into a single value which is then used to evaluate components for ductile failure. Equivalent stresses are used in evaluating pressure vessels for protection against plastic collapse in the ASME Code.
The ratio between the hydrostatic and equivalent stress is referred to as the triaxiality ratio. When this ratio increases, the plastic strain required to cause rupture decreases exponentially. At high levels of triaxiality ratios, the material basically doesn’t have anywhere to plastically deform to causing it to fail in a brittle manner. This is the reason for the requirement of evaluating a component for local failure in the ASME Code.
As stated earlier, this type of failure will not be predicted by performing an evaluation for protection against plastic collapse in accordance with the ASME Code. With hydrostatic stress, the three principal stresses are equal in magnitude. Evaluation for protection against failure due to plastic collapse uses the equivalent stress (von Mises) criteria. An inspection of the equation for equivalent stress (shown below) shows when the three principal stresses are equal, the equivalent stress will (always) be equal to zero.
Because of this, the ASME Code requires pressure vessel components to be evaluated for this type of failure mechanism, which it calls local failure.
Evaluation for Local Failure
As of the 2023 Edition of the ASME Boiler & Pressure Vessel Code, components can be evaluated for local failure using either elastic analysis, or elastic-plastic analysis. With the elastic analysis method, the sum of the three principal stresses is compared to an allowable stress limit. The elastic-plastic analysis method compares the sum of the equivalent plastic strain and forming strain to a limiting triaxial strain.
Closing Remarks
In order for local failure to occur, significant stresses must be developed in the three orthogonal directions. As a result of this, local failure is more likely to occur in thick-walled pressure vessels and components than thin-walled pressure vessels. While local failure is rare for thin-walled pressure vessels, it is a real failure mechanism and ensuring that it will not occur is required by the ASME Code.